Non-blocking Transactional Atomicity
28 May 2013
tl;dr: You can perform non-blocking multi-object atomic reads and writes across arbitrary data partitions via some simple multi-versioning and by storing metadata regarding related items.
N.B. This is a long post, but it’s comprehensive. Reading the first third will give you most of the understanding.
Edit 4/2014: We wrote a SIGMOD paper on these ideas! Check it out or read an updated post on the new algorithms.
Performing multi-object updates is a common but difficult problem in real-world distributed systems. When updating two or more items at once, it’s useful for other readers of those items to observe atomicity: either all of your updates are visible or none of them are.1 This crops up in a bunch of contexts, from social network graphs (e.g., Facebook’s Tao system, where bi-directional “friend” relationships are stored in two uni-directional pointers) to distributed data structures like counters (e.g., Twitter’s Rainbird hierarchical aggregator) and secondary indexes (a topic for a future post). In conversations I’ve had regarding our work on Highly Available Transactions, atomic multi-item update, or transactional atomicity, is often the most-requested feature.
Existing Techniques: Locks, Entity Groups, and “Fuck-it Mode”
The state of the art in transactional multi-object update typically employs one of three strategies.
-
Use locks to update multiple items at once. Grab write locks on update and read locks for reads and you’ll ensure transactional atomicity. However, in a distributed environment, the possibility of partial failure and network latency means locking can lead to a Bad Time™.2
-
Co-locate distributed objects you’d like to update together. This strategy (often called “entity groups”) makes transactional atomicity easy: locking on a single machine is fast and not subject to the problems of distributed locking under partial failure and network latency. Unfortunately, this solution impacts data layout and distribution and does not work well for data that is difficult to partition (social networks, anyone?).
-
Use “fuck-it mode,” whereby you simultaneously update all keys without any concurrency control and hope readers observe transactional atomicity. This final option is remarkably common: it scales well and is applicable to any system, but it doesn’t provide any atomicity guarantees until the system stabilizes (i.e., converges, or is eventually consistent).
In this post, I’ll provide a simple alternative (let’s call it Non-blocking Transactional Atomicity, or NBTA) that uses multi-versioning and some extra metadata to ensure transactional atomicity without the use of locks. Specifically, our solution does not block readers or writers in the event of arbitrary process failure and, as long as readers and writers can contact a server for each data item they want to access, the system can guarantee transactional atomicity of both reads or writes. At a high level, the key idea is to avoid performing in-place updates and to use additional metadata to substitute for synchronous synchronization across replicas.
NBTA by Example
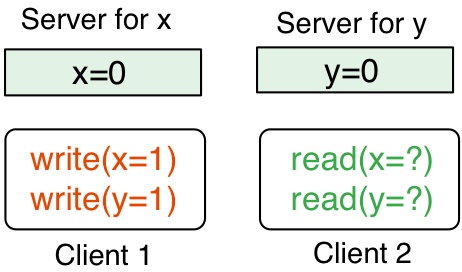
To illustrate the NBTA algorithm, consider the simple scenario where
there are two servers, one storing item x and the other storing item
y, both of which have value 0. Say we have two clients, one of
which wishes to write x=1, y=1 and another that wants to read x
and y together (i.e., x=y=0 or x=y=1). (We’ll discuss
replication later.)
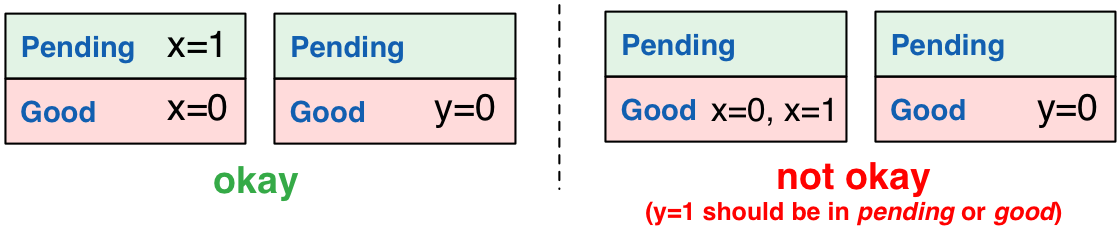
good, pending, and Invariants
Let’s split each server’s storage into two parts: good and
pending. We will maintain the invariant that every write stored in
good will have its transactional sibling writes (i.e., the other
writes originating from the transactionally atomic operation) present
on each of their respective servers, either in good or
pending. That is, if x=1 is in good on the server for x, then,
in the example above, y=1 will be guaranteed to be in good or
pending on the server for y.
To maintain the above invariant, servers first place writes into
pending. Then, once servers learn (possibly asynchronously) that a
write’s transactional siblings are all in pending (let’s call this
process “learning that a write is stable”), the servers individually
move their respective writes into good. One simple strategy for
informing servers that a write is stable is to have the writing client
perform two rounds of communication: the first round places writes
into pending, then, once all servers have acknowledged writes to
pending, the client notifies each server that its write is
stable. (If you’re nervous, this isn’t two-phase commit; more on that
later.)

Races and Pointers
We’re almost done. If readers read from good, then they’re
guaranteed to be able to read transactional siblings from other
servers. However, there’s a race condition: what if one server has
placed its write in good but another still has its transactional
sibling in pending? We need a way to tell the second server to serve
its read from pending.

To handle this race condition, we attach additional information to
each write: a list of transactional siblings. At the start of a
multi-key update, clients generate a unique timestamp for all of their
writes (say, client ID plus local clock or random hash), which they
attach to each write, along with a list of the keys written to in the
transaction. Now, when a client reads from good, it will have a list
of transactional siblings with the same timestamp. When the client
requests a read from one of those sibling items, the server can fetch
it from either pending or good. If a client doesn’t need to read a
specific item, the server can respond with the highest timestamped
item from good.
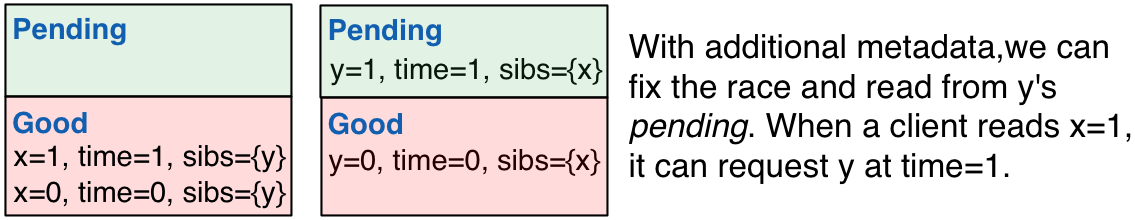
Putting it all together
We now have an algorithm that guarantees that all writes in a
multi-key update are accessible before revealing them to readers. If a
reader accesses a write, it is guaranteed to be able to access its
transactional siblings without blocking. This way, readers will never
stall waiting for a sibling that hasn’t arrived on its respective
server. To make sure readers can access siblings in both good and
pending, we attached additional metadata to each write that can be
used by servers in the event of skews in stable write detection across
servers. If readers or writers fail, there is no effect on other
readers or writers. Any partially written multi-key updates will never
become stable, and servers can optionally guarantee write stability by
performing pending acknowledgments (i.e., performing the second
phase of the client write) for themselves.
It Gets Better!
…because optimizations are awesome…
There are several optimizations and modifications we can make to the NBTA protocol:
-
Size of
pendingandgood: if users want “last writer wins” semantics, there’s no need to store more than one write ingood. However, if we do this, a write’s sibling may have been overwritten. If we want to prevent readers from reading “forwards in time” (e.g., readx=0theny=1thenx=1, which preserves the property that once one write becomes visible, all of transaction’s writes become visible but does not guarantee a consistent snapshot across items), then servers can retain items ingoodfor a bounded amount of time (e.g., as long as a multi-item read might take) and/or clients can retry reads in the presence of overwrites. -
Faster writes: As I alluded to above, it’s not necessary to have the client perform the second round of communication (which requires three message delays until visibility). Instead, servers can directly contact one another once they’ve placed writes in
pending, requiring only two message delays. Alternatively, clients can issue the second round of communication asynchronously. However, to ensure that clients read their writes in these scenarios, they need to retain metadata until they have (asynchronously) detected that each write is ingood. -
Replication: So far, I’ve only discussed having a single server for each data item. With “strong consistency” (i.e., linearizability) per server, the above algorithm works fine. With asynchronous, or lazy, replication between servers (e.g., “eventual consistency”), there are two options. If all clients contact disjoint sets of servers (e.g., all clients in a datacenter contact a full set of replicas), then clients only need to update their local set of servers, and each set of servers can detect when writes are stable within their groups. However, if clients can connect to any server, then writes should only become stable whenever all respective servers have placed their writes in
goodorpending. This can take indefinitely long in the presence of partial failure.3 -
Read/write transactions: I’ve discussed read-only and write-only transactions here, but it’s easy to use these techniques for general-purpose read/write transactions. The main problem when aiming for models like ANSI Repeatable Read (i.e., snapshot reads) is ensuring that reads come from a transactionally atomic set: this can be done by pre-declaring all reads in the transaction and fetching all items at the start of the transaction or via fancier (and more expensive) metadata like vector clocks, which I won’t get into here.
-
Metadata sizes: The metadata required above is linear in the number of keys written. This is modest in practice, but metadata can also be dropped once all sibling writes are present in
good(i.e., there is no race condition for the transactional writes).
…and it works in real life.
We’ve built a database based on LevelDB that implements NBTA with all of the above optimizations except metadata pruning (related pseudocode here). Under the Yahoo! Cloud Serving Benchmark, NBTA transactions of 8 operations each achieve within 33% (all writes) to 4.8% (all reads) of the peak throughput of eventually consistent (i.e., “fuck-it”) operation (with 3.8–48% higher latency). Our implementation scales linearly, to over 250,000 operations per second for transactions of length 8 consisting of 50% reads and 50% writes on a deployment of 50 EC2 instances.
In our experience, NBTA performs substantially better than lock-based
operation because there is no blocking involved. The two primary
sources of overhead are due to metadata (expected to be small for
real-world transactions like the Facebook and secondary indexing) and
moving writes from pending to stable (if, as in our
implementation, writes to pending are persistent, this results in
two durable server-side writes for every client-initiated
write). Given these results, we’re excited to start applying NBTA to
other data stores (and secondary indexing).
So what just happened?
If you’re a distributed systems or database weenie like me, you may be curious how NBTA relates to well-known problems like two-phase commit.
The NBTA algorithm is a variant of uniform reliable broadcast with
additional metadata to address the case where some servers have
delivered writes but others have not yet, providing safety (e.g., see
Algorithm
3.4). Formally,
NBTA as presented here does not guarantee termination: servers may not
realize that a write in pending will never become
stable. Recognizing a “dead write” in pending requires failure
detection and, in practice, writes can be removed from pending once
sibling servers have been marked as dead, the server detects that a
client died mid-write, the write (under last-writer-wins semantics) is
overwritten by a higher timestamped write in good, or, more
pragmatically, after a timeout.
As presented here, servers don’t abort updates, but this isn’t
fundamental. Instead of placing items in pending, servers can
instead reject updates, so any updates that were placed into pending
on other servers will never become stable. NBTA is weaker than
traditional non-blocking atomic commitment
protocols
because it allows non-termination for individual transactional updates
(that is, garbage collecting pending may take a while). The trick is
that, in practice, as long as independent transactional updates can be
executed concurrently (as is the case with last-writer-wins and as is
the case for all Highly Available
Transaction)
semantics, a stalled transactional update won’t affect other
updates. In contrast, traditional techniques like two-phase commit
with two-phase locking will require stalling in the presence of
coordinator failure.
There are several ideas in the database literature that are similar to NBTA. The optimization for reducing message round trips is similar to the optimizations employed by Paxos Commit, while the use of additional metadata to guard against concurrent updates may remind you of B-link trees or other lockless data structures. And, of course, multi-version concurrency control and timestamp-based concurrency control have a long history in database systems. The key in NBTA is to achieve transactional atomicity while avoiding a centralized timestamp authority or concurrency control mechanism.
All this said, I haven’t seen a distributed transactional atomicity algorithm like NBTA before; if you have, please do let me know.
Conclusion
This post demonstrated how to achieve atomic multi-key updates across arbitrary data partitions without using locks or losing the ability to provide a safe response despite arbitrary failures of readers, writers, and (depending on the configuration) servers. The key idea was to establish an invariant that all writes have to be present on the appropriate servers before showing them to readers. The challenge was in solving a race condition between showing writes on different servers—trivial for locks but harder for a highly available system. And it works in practice–rather well, and much better than similar lock-based techniques! If you’ve made it this far, you’ve probably followed along, but I look forward to following up with a post on how to perform consistent secondary indexing via similar techniques—a potential killer application for NBTA, particularly given that it’s often considered impossible in scalable systems.
As always, feedback is welcomed and encouraged. If you’re interested in these algorithms in your system, let’s talk.
Thanks to Peter Alvaro, Neil Conway, Aurojit Panda, and Shivaram Venkataraman, and Reynold Xin for early feedback on this post. This research is joint work with Aaron Davidson, Alan Fekete, Ali Ghodsi, Joe Hellerstein, and Ion Stoica at UC Berkeley and the University of Sydney.
[1] Note that this “atomicity” is not the same as linearizability, the data consistency property addressed in Gilbert and Lynch’s proof of the CAP Theorem and often referred to as “atomic” consistency. Linearizability concerns ordering operations with respect to real time and is a single-object guarantee. The “atomicity” here stems from a database context (namely, the “A” in “ACID” and concerns performing and observing operations over multiple objects. To avoid further confusion, we’ll call this “atomicity” “transactional atomicity.”
\[2\] More specifically, there are a bunch of ways things can get weird. If a client dies while holding locks, then the servers should eventually revoke the locks. This often requires some form of failure detection or timeout, which leads to awkward scenarios over asynchronous networks, coupled with effective unavailability prior to lock revocation. In a linearizable system, as in the example, we've already given up on availability, so this isn't necessarily horrible---but it's a shame (read: it's slow) to block readers during updates and vice-versa. If we're going for a highly available (F=N-1 fault-tolerant) setup (as we will later on), locks are a non-starter; locks are fundamentally at odds with providing available operation on all replicas during partitions.
\[3\] Hold up, cowboy! What does this replication mean for availability? As I'll discuss soon, we haven't talked about when the effects of transactions will become visible in the event of replica failures (i.e., when people will read my writes). Readers will *always* be able to read transactionally atomic sets of data items from non-failing replicas; however, depending on the desired availability, reads may not be the most "up to date" set that is available on some servers. One way to look at this trade-off is as follows:
- You can achieve linearizability and transactional atomicity, whereby everyone sees all writes after they complete, but writes may take an indefinite amount of time to complete ("CP")
- You can achieve read-your-writes and transactional atomicity, whereby you can see your writes after they complete, but you'll have to remain "sticky" and continue to contact the same (logical) set of servers during execution (your "sticky" neighboring clients will also see your writes; "Sticky-CP")
- You can achieve transactional atomicity and be able to contact any server, but writes won't become visible until all servers you might read from have received the transactional writes ("AP"; at the risk of sub-footnoting myself, I'll note that there are cool and useful connections to different kinds of [failure detectors](http://pine.cs.yale.edu/pinewiki/FailureDetectors) here).
Read More
- How To Make Fossils Productive Again (30 Apr 2016)
- You Can Do Research Too (24 Apr 2016)
- Lean Research (20 Feb 2016)
- I Loved Graduate School (01 Jan 2016)
- NSF Graduate Research Fellowship: N=1 Materials for Systems Research (03 Sep 2015)
- Worst-Case Distributed Systems Design (03 Feb 2015)
- When Does Consistency Require Coordination? (12 Nov 2014)
- Data Integrity and Problems of Scope (20 Oct 2014)
- Linearizability versus Serializability (24 Sep 2014)
- MSR Silicon Valley Systems Projects I Have Loved (19 Sep 2014)